Bridgesk's Blog
0%

SUSCTF2022复盘

发表于 更新于 分类于

DigitalCircuits

该文件为python打包成的exe文件，可以用如下方法判断：

1、python打包成的文件通常的图标都是python模样

2、用ExeinfoPe查看文件

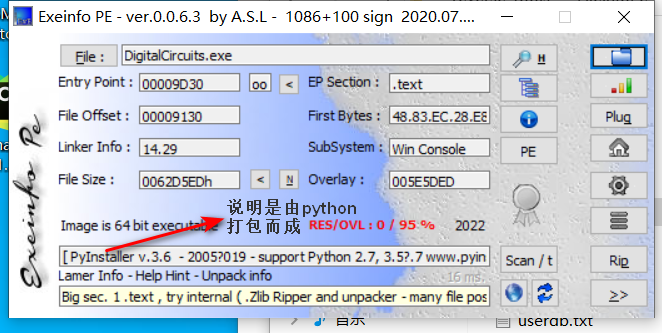
3、ida载入文件，shift+f12查看字符串

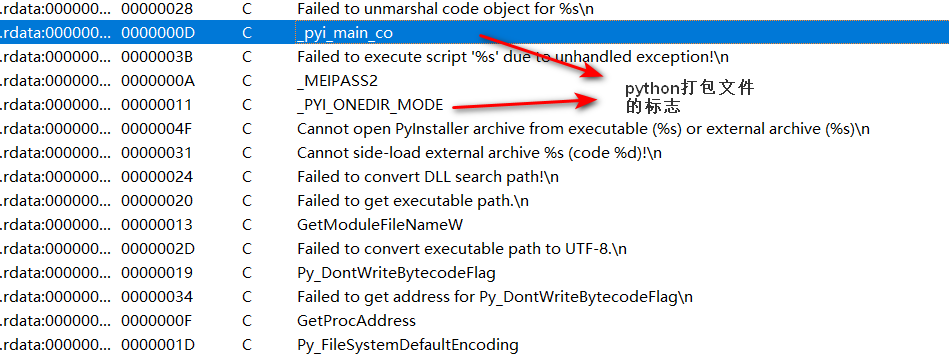
判断出这一点，接下来我们的任务就是将.exe文件反编译出python源码了

参考这篇文章：(别再问我exe反编译成Python脚本了！ - 云+社区 - 腾讯云 (tencent.com))

首先通过pyinstxtractor.py脚本提取pyc文件，引用参考文章中的方法

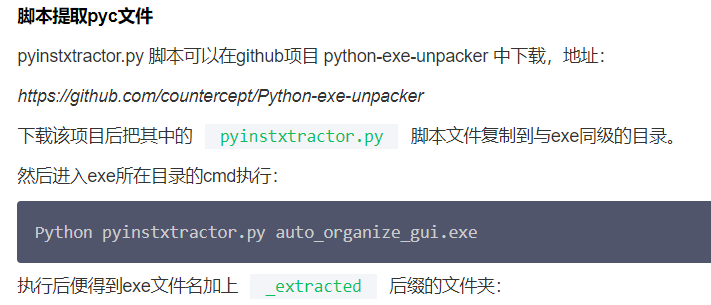
执行命令

1
python pyinstxtractor.py DigitalCircuits.exe

运行结果如下

生成了一个名为DigitalCircuits.exe_extracted的文件夹

在文件夹内可以找到与可执行文件同名的.pyc文件，不过需要手动补后缀

下一步是还原文件头

将pyc文件与同目录下的struct文件用十六进制编辑器打开对比

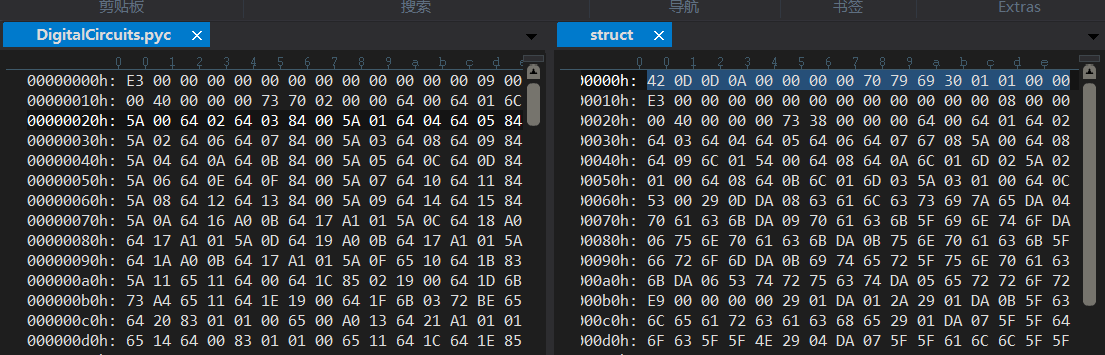
发现缺少第一行的16个字节

先插入16个字节，再将struct中的第一行复制到pyc文件中

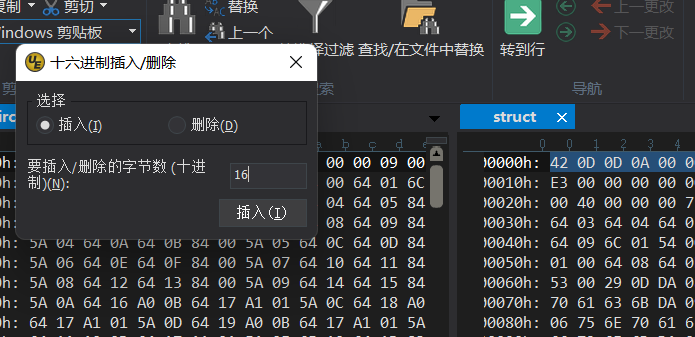
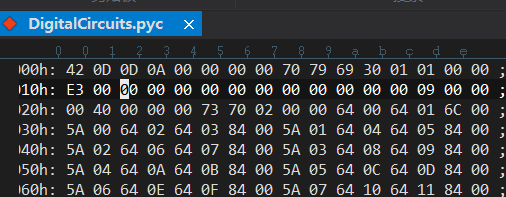
保存，然后通过uncompyle6将pyc文件反编译为py文件

1
uncompyle6 -o DigitalCircuits.py DigitalCircuits.pyc

代码如下，注释为个人分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
# uncompyle6 version 3.7.4
# Python bytecode 3.7 (3394)
# Decompiled from: Python 3.7.9 (tags/v3.7.9:13c94747c7, Aug 17 2020, 18:58:18) [MSC v.1900 64 bit (AMD64)]
# Embedded file name: DigitalCircuits.py
# Compiled at: 1995-09-28 00:18:56
# Size of source mod 2**32: 257 bytes
import time

def f1(a, b):#与运算
    if a == '1':
        if b == '1':
            return '1'
    return '0'


def f2(a, b):#或运算
    if a == '0':
        if b == '0':
            return '0'
    return '1'


def f3(a):#非运算
    if a == '1':
        return '0'
    if a == '0':
        return '1'


def f4(a, b):#异或运算
    return f2(f1(a, f3(b)), f1(f3(a), b))


def f5(x, y, z):#全加器，s为和，c为进位
    s = f4(f4(x, y), z)
    c = f2(f1(x, y), f1(z, f2(x, y)))
    return (s, c)


def f6(a, b):
    ans = ''
    z = '0'
    a = a[::-1]#将a串逆序
    b = b[::-1]#将b串逆序
    for i in range(32):
        ans += f5(a[i], b[i], z)[0]#按位相加存入ans
        z = f5(a[i], b[i], z)[1]

    return ans[::-1]#返回ans的逆序


def f7(a, n):
    return a[n:] + '0' * n


def f8(a, n):
    return n * '0' + a[:-n]


def f9(a, b):
    ans = ''
    for i in range(32):
        ans += f4(a[i], b[i])

    return ans


def f10(v0, v1, k0, k1, k2, k3):#k0，k1，k2，k3均为常量，递归求解v0，v1
    s = '00000000000000000000000000000000'
    d = '10011110001101110111100110111001'
    for i in range(32):
        s = f6(s, d)
        v0 = f6(v0, f9(f9(f6(f7(v1, 4), k0), f6(v1, s)), f6(f8(v1, 5), k1)))
        v1 = f6(v1, f9(f9(f6(f7(v0, 4), k2), f6(v0, s)), f6(f8(v0, 5), k3)))

    return v0 + v1


k0 = '0100010001000101'.zfill(32)
k1 = '0100000101000100'.zfill(32)
k2 = '0100001001000101'.zfill(32)
k3 = '0100010101000110'.zfill(32)
flag = input('please input flag:')
if flag[0:7] != 'SUSCTF{' or flag[(-1)] != '}':
    print('Error!!!The formate of flag is SUSCTF{XXX}')
    time.sleep(5)
    exit(0)
flagstr = flag[7:-1]
if len(flagstr) != 24:#flagstr长度为24
    print('Error!!!The length of flag 24')
    time.sleep(5)
    exit(0)
else:
    res = ''
    for i in range(0, len(flagstr), 8):#每次传入flagstr中的8位，共能循环3次
        v0 = flagstr[i:i + 4]
        v0 = bin(ord(flagstr[i]))[2:].zfill(8) + bin(ord(flagstr[(i + 1)]))[2:].zfill(8) + bin(ord(flagstr[(i + 2)]))[2:].zfill(8) + bin(ord(flagstr[(i + 3)]))[2:].zfill(8)
        v1 = bin(ord(flagstr[(i + 4)]))[2:].zfill(8) + bin(ord(flagstr[(i + 5)]))[2:].zfill(8) + bin(ord(flagstr[(i + 6)]))[2:].zfill(8) + bin(ord(flagstr[(i + 7)]))[2:].zfill(8)
        res += f10(v0, v1, k0, k1, k2, k3)

    if res == '001111101000100101000111110010111100110010010100010001100011100100110001001101011000001110001000001110110000101101101000100100111101101001100010011100110110000100111011001011100110010000100111':
        print('True')
    else:
        print('False')
time.sleep(5)

解题脚本如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
def f1(a, b):#与运算
    if a == '1':
        if b == '1':
            return '1'
    return '0'


def f2(a, b):#或运算
    if a == '0':
        if b == '0':
            return '0'
    return '1'


def f3(a):#非运算
    if a == '1':
        return '0'
    if a == '0':
        return '1'


def f4(a, b):#异或运算
    return f2(f1(a, f3(b)), f1(f3(a), b))


def f5(x, y, z):#全加器，s为和，c为进位
    s = f4(f4(x, y), z)
    c = f2(f1(x, y), f1(z, f2(x, y)))
    return (s, c)


def f6(a, b):
    ans = ''
    z = '0'
    a = a[::-1] #a逆序
    b = b[::-1] #b逆序
    for i in range(32):
        ans += f5(a[i], b[i], z)[0]
        z = f5(a[i], b[i], z)[1]

    return ans[::-1]


def f6_decode(a, c):#运用二进制运算的性质，通过补码求减

    c = int(c, 2) + (1 << 32)
    a = int(a, 2)
    b = (c - a) % (1 << 32)
    return str(bin(b)[2:].zfill(32))


def f7(a, n):#舍弃前n个元素，在末尾补0
    return a[n:] + '0' * n


def f8(a, n):
    return n * '0' + a[:-n]#舍弃后n个元素，在开头补0


def f9(a, b): #按位异或
    ans = ''
    for i in range(32):
        ans += f4(a[i], b[i])

    return ans


def f10(v0, v1, k0, k1, k2, k3):
    s = '00000000000000000000000000000000'
    d = '10011110001101110111100110111001'
    for i in range(32):
        s = f6(s, d)
        v0 = f6(v0, f9(f9(f6(f7(v1, 4), k0), f6(v1, s)), f6(f8(v1, 5), k1)))
        v1 = f6(v1, f9(f9(f6(f7(v0, 4), k2), f6(v0, s)), f6(f8(v0, 5), k3)))
    return v0+v1

def f10_decode(res, k0, k1, k2, k3):
    v0 = res[0:32]
    v1 = res[32:64]
    s = '11000110111011110011011100100000'
    d = '10011110001101110111100110111001'
    for i in range(32):
        v1 = f6_decode(f9(f9(f6(f7(v0, 4), k2), f6(v0, s)), f6(f8(v0, 5), k3)), v1)
        v0 = f6_decode(f9(f9(f6(f7(v1, 4), k0), f6(v1, s)), f6(f8(v1, 5), k1)), v0)
        s = f6_decode(d, s)
    return v0+v1


k0 = '0100010001000101'.zfill(32) #Python zfill() 方法返回指定长度的字符串，原字符串右对齐，前面填充
k1 = '0100000101000100'.zfill(32)
k2 = '0100001001000101'.zfill(32)
k3 = '0100010101000110'.zfill(32)
res = '0011111010001001010001111100101111001100100101000100011000111001'\
      '0011000100110101100000111000100000111011000010110110100010010011' \
      '1101101001100010011100110110000100111011001011100110010000100111'
flag = ''
res1 = res[0:64]
res2 = res[64:128]
res3 = res[128:192]
flag += f10_decode(res1, k0, k1, k2, k3)
flag += f10_decode(res2, k0, k1, k2, k3)
flag += f10_decode(res3, k0, k1, k2, k3)
for i in range(0, len(flag), 8):
    a = int(flag[i:i+8], 2)
    print(chr(a), end='')

更新：

看了大佬们的wp才发现这是个tea加密算法，只不过是二进制的而已，套用tea解密的脚本即可求得flag

这里贴的是Dest0g3 Team的脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def tea_decode(enc, k):
    v0 = enc[0]
    v1 = enc[1]
    sum = (delta*32)&0xffffffff
    for i in range(32):
        v1 -= ((v0<<4) + k[2]) ^ (v0 + sum) ^ ((v0>>5) + k[3])
        v1 &= 0xffffffff
        v0 -= ((v1<<4) + k[0]) ^ (v1 + sum) ^ ((v1>>5) + k[1])
        v0 &= 0xffffffff
        sum -= delta
    return (v0, v1)

enc = '001111101000100101000111110010111100110010010100010001100011100100110001001101011000001110001000001110110000101101101000100100111101101001100010011100110110000100111011001011100110010000100111'
enc = [int(enc[i:i+32], 2) for i in range(0, len(enc), 32)]

k = [0]*4
k[0] = int('0100010001000101'.zfill(32), 2)
k[1] = int('0100000101000100'.zfill(32), 2)
k[2] = int('0100001001000101'.zfill(32), 2)
k[3] = int('0100010101000110'.zfill(32), 2)
delta = int('10011110001101110111100110111001', 2)

flag = b''
for i in range(0, len(enc), 2):
    ans = tea_decode(enc[i:i+2], k)
    flag += ans[0].to_bytes(4, 'big')+ans[1].to_bytes(4, 'big')#int.to_bytes(length, byteorder)

print(b'SUSCTF{'+flag+b'}')

Hell_world

​ 这道题比赛的时候没有思路，刚刚照着大佬们的wp复现了一下，虽然只是懂了个大概，但还是记录一下

​ 引用SU战队的话，“跟西湖论剑题目gghdl差不多 就是改了下case结构和数据可以根据链接来解题”

​ 拿到程序，ida打开后首先shift+f12搜索字符串，search含有flag

的字符串

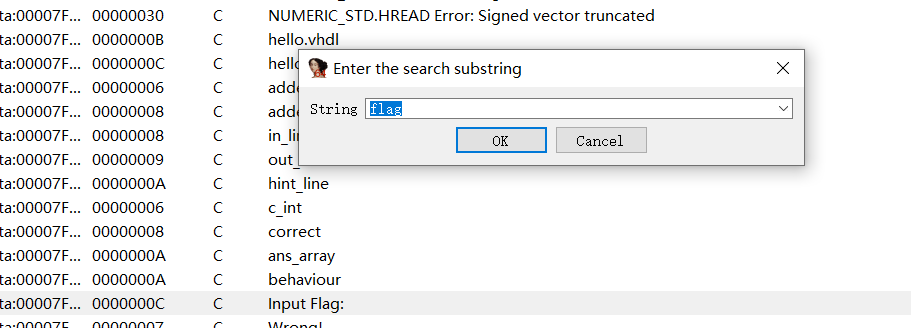
之后就是解析每个case函数的作用

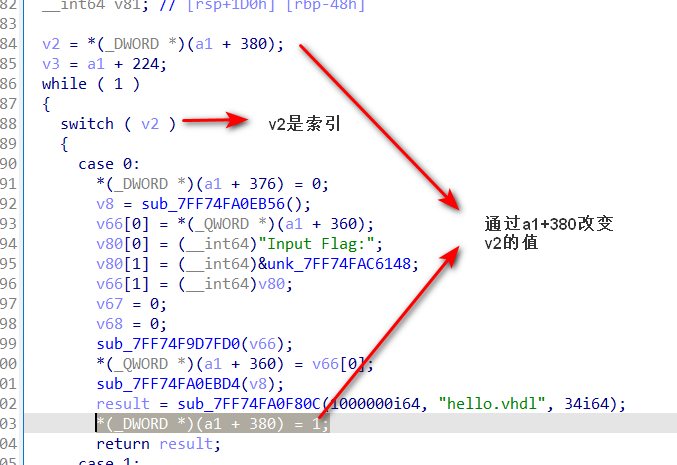
然后我们通过动态调试的方法找到读取输入的函数

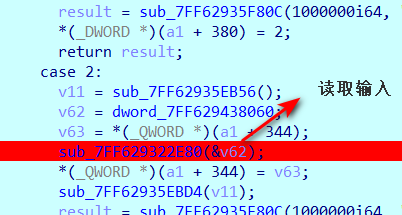
再分析case3

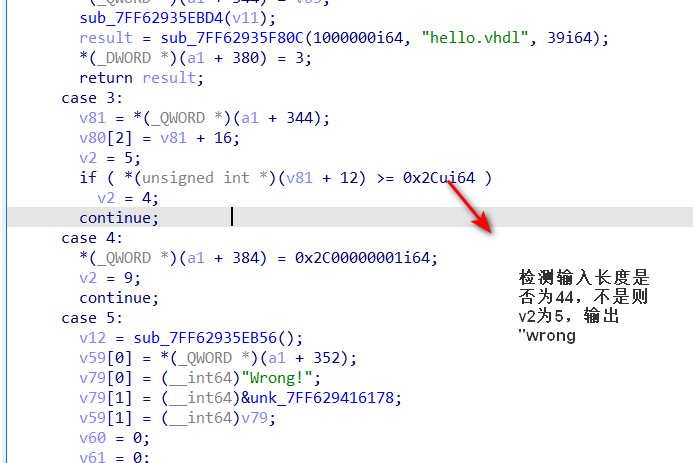
如果输入长度是44位的话就执行case4，进而执行case9，所以推测case9是加密函数

在分析case9之前，先查看输出正确的条件

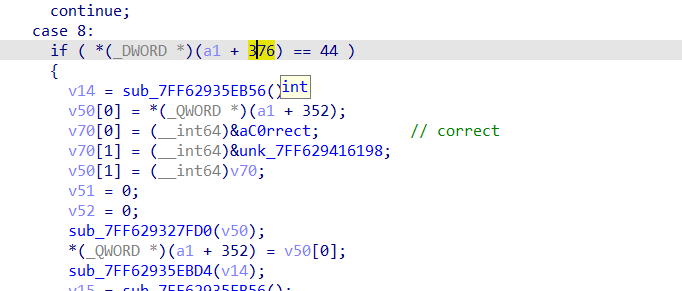
正确条件为*(_DWORD )(a1 + 376) == 44，因此我们需要查看修改(_DWORD *)(a1 + 376) 值的位置，发现只在case11中出现

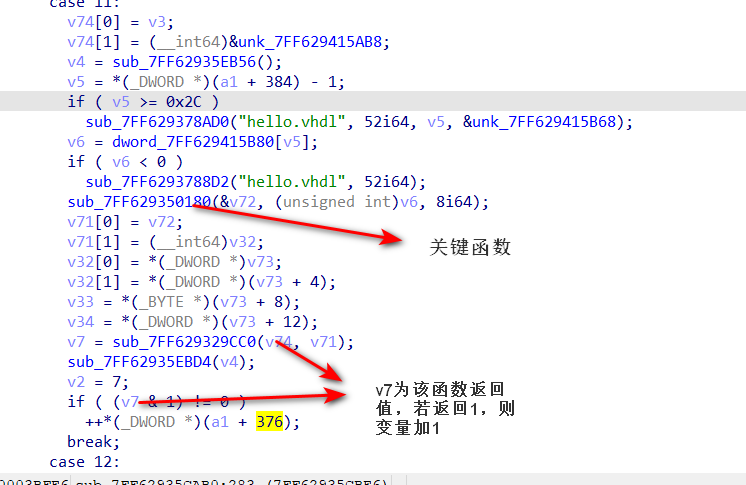
追踪传入sub_7FF629329CC0函数的v74， v71，可以追踪到图中标出的关键函数，此函数在程序中共调用了3次，另外两次分别在case10和case9中，其中case9的该函数传入的为我们输入的数据(存在a1中)

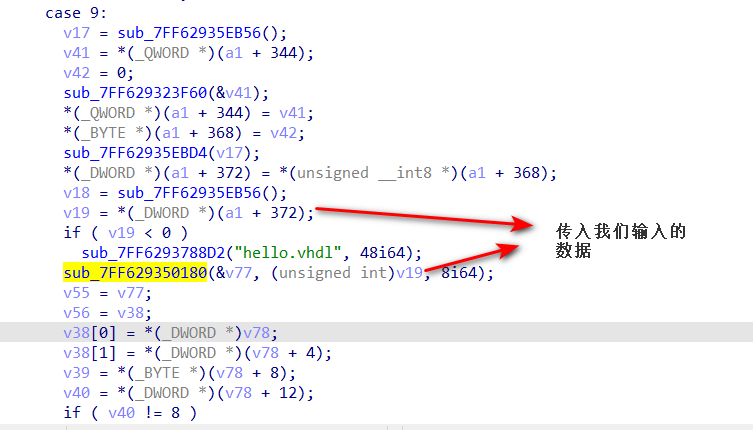
因此我们可以动态调试分析该函数的功能，传入字符串0123456789qwertyuiopasdfghjklzxcvbnmQWERTYUI

常用字符0123456789qwertyuiopasdfghjklzxcvbnmQWERTYUIOPASDFGHJKLZXCVBNM{}_-

运行case9中的sub_7FF629350180函数,查看对应的汇编代码

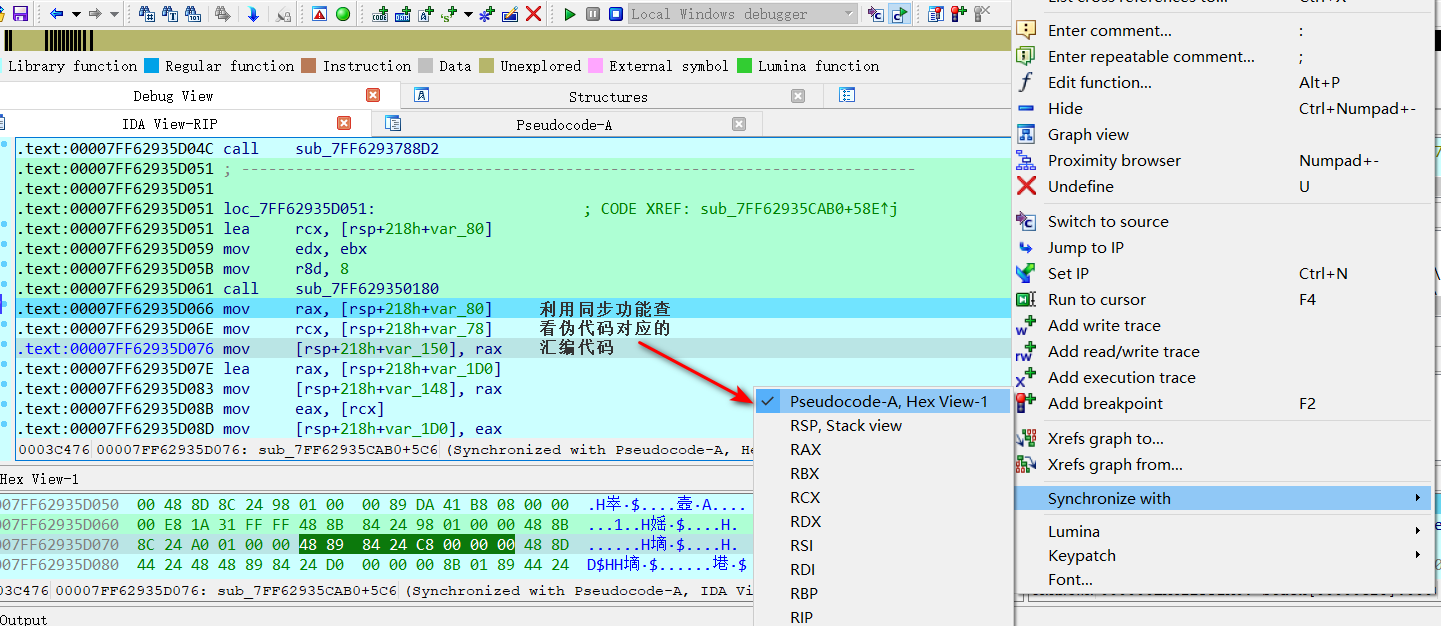
查看函数返回值（存在rax寄存器中）

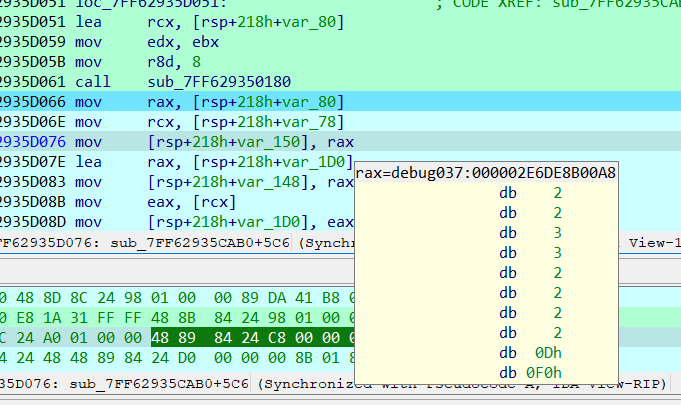
其中22332222即为传入字符串中0对应的二进制码00110000每位加二，所以函数的功能其实就是字符串转换为对应的二进制

再查看sub_7FF629329CC0函数的汇编代码，发现就是异或运算

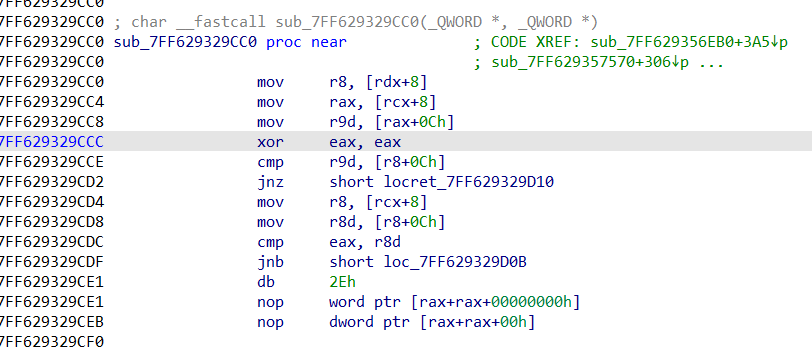
所以flag就是将dword_7FF629415B80和dword_7FF629415C50中的数据异或即可